摘 要:目的预测混凝土结构早龄期开裂的可能性. 方法以可靠度理论为基础,建立了混凝土结构早龄期开裂的分析模型,利用开裂概率和临界开裂风险来分析与预测混凝土结构早龄期的开裂情况,并将分析模型在混凝土挡土墙工程中应用. 结果混凝土挡土墙分析模型的预测结果与观测结果基本一致. 结论应用开裂概率和临界开裂风险来分析与预测混凝土结构早龄期开裂,可以优选混凝土材料的组成,尽量减少混凝土结构早龄期的开裂.
关键词:混凝土结构;开裂概率;临界开裂风险;早龄期;预测
中图分类号: TU528 文献标识码:A
混凝土结构的耐久性评价一般是以混凝土结构没有明显的可见裂缝为前提,如果混凝土在硬化过程中产生可见的裂缝,那么混凝土结构的耐久性评价将受到影响,混凝土结构使用寿命预测的可信度将会降低. 早龄期结构中的混凝土在受限条件下因水化硬化而导致其体积发生变化(一般是收缩) 是混凝土结构早龄期开裂的主要原因[1 ] ,正如Springenschmid 所说[2 ] :“避免混凝土早龄期裂缝是当前混凝土技术的主要问题之一,采用现代的概念预测混凝土早龄期的应力及其影响,来代替单纯依据现场经验的方法”. 以可靠度理论为基础的结构设计与旧建筑物评价是结构工程研究的热点之一,但对混凝土结构非服役期的早龄期开裂问题的研究却相对较少, F. Czerny[3 ]等利用概率方法分析了避免混凝土早龄期开裂的安全系数. 袁勇等[4 ]建立了考虑热应力,干燥收缩和徐变等因素的混凝土早龄期开裂的计算公式,笔者在上述的研究基础上以可靠度理论为基础,建立了混凝土结构早龄期开裂的分析模型,计算了混凝土结构早龄期的开裂概率和临界开裂风险,来预测混凝土结构早龄期开裂的可能性,指导工程实践.
1 理论基础
1.1 开裂概率
在混凝土早龄期开裂分析中,影响因素很多,主要包括温度、收缩和徐变等因素. 开裂的主要问题一个是阻止开裂的抵抗参数r ,另一个荷载参数s ,其功能函数关系式为[5 ]
Θ= r - s ≥0 (1)
当r 和s 这两个参数可以被认为是服从正态分布的随机变量,它们的数学期望为ur 和us ,标准方差为σr 和σs ,因此有概率P[Θ = r - s < 0 ] ,可靠指标β为
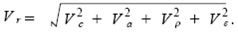
在实际工程中,功能函数不一定服从正态分布,为计算可靠指标,需要将功能函数近似地看成服从正态分布的随机变量,因为当破坏概率较大时,开裂概率对功能函数的分布类型不敏感,可以近似地取正态分布. 可靠指标的计算有多种方法,其中最简单的方法是中心点法,笔者利用中心点法确定实际工程中混凝土早龄期时的开裂概率.
1.2 临界开裂风险
1.2.1 抗力参数
由Êstlund[6 ]提出抗力的表达式为
r = Caρε (3)
式中: C 为表征计算方法不确定性的参数,数学期望为uc ,变异系数为V c ; a 为几何参数,数学期望为ua ,变异系数为V a ;ρ为混凝土应变系数,数学期望为uρ,变异系数为Vρ;ε为混凝土最终应变,数学期望为uε,变异系数为Vε;抗力的数学期望为ur = ucuauρuε,变异系数,忽略高次项时,为
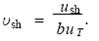
1.2.2 荷载参数
混凝土在早龄期时的荷载考虑应变时有
s = γR ( bεT +εsh) (4)
式中:γR 为约束系数,0 ≤γR ≤1 ;εT 为由结构内部温度变化引起的非弹性应变, 数学期望为, u T变异系数为V T ;εsh 为收缩引起的应变,数学期望为ush , b 变异系数为V sb ; b 为常量, b ≥0. 一般认为随机变量εT 和εsh 服从正态分布,所以有us =γR ( bu T + ush) , 为了讨论方便设定常数

1.2.3 计算过程
功能函数中涉及两类随机变量,抗力的随机变量服从对数正态分布,荷载的随机变量服从正态分布. 根据实际条件选取参数:安全等级β,各变量的变异系数V T , V sh , V c , Vε , V a , Vρ; 常数υsh , Kc , Ka , Kρ , Kε , KT .
(1) 确定敏感系数
功能函数Θ = rd - sd = rd - γR ( bεT +εs h ) ,设定辅助常量κr ,κT ,κsh且

抗力、温度变化和收缩的敏感系数分别定义为
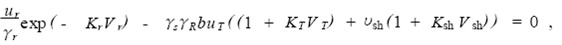
(2) 计算部分系数
当Θ = 0 时,
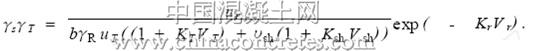
得
混凝土的开裂风险[7 ]应满足下式:
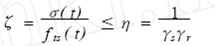
式中:ζ为开裂风险;σ( t ) 为t 时刻混凝土受到的拉应力; f ts ( t) 为t 时刻混凝土的抗拉强度;η为临界开裂风险.
2 工程应用
某地铁工程的挡土墙,浇筑混凝土的试验段长110 m. 1 # 混凝土和2 # 混凝土的强度等级为C30 ,混凝土抗压强度的标准方差参考文献[ 8 ]已给出,取抗拉强度的标准方差与其抗压强度的标准方差相同,混凝土配合比和内应力见文献[ 9 ] ,内应力的变异系数与抗拉强度的变异系数相同,
利用中心点法计算可靠指标和开裂概率的结果如表1 所示.
表1 挡土墙开裂概率

可以看出,1 # 混凝土墙的开裂概率7 d龄期时,开裂概率已达到0148 ,表明混凝土开裂的可
能性非常大. 2 # 混凝土7 d 龄期时开裂概率为010024 ,根据文献[10 ]在施工期可以认为2 # 混凝土是安全的.
混凝土挡土墙的设计参数如表2 所示,计算的临界开裂风险如表3 所示. 从图1 可以看出,1 # 混凝土4 d左右时,开裂风险就超过临界开裂风险,2 # 混凝土的开裂风险在考查的龄期内一直小于临界开裂风险. 在实际施工时1 # 混凝土在4 d左右时发生开裂,而2 # 混凝土一直处于良好状态.
表2 设计参数


3 结 语
建立混凝土结构早期开裂的分析模型,模型中考虑了混凝土材料性能、结构特点等因素的随机性,引入开裂概率和临界开裂风险来分析混凝土结构早龄期开裂的可能性,并在实际工程中获得应用,尽量减少混凝土结构的早龄期开裂现象.
参考文献:
[1] 王甲春,阎培渝. 硅酸盐水泥- 粉煤灰复合胶凝材料体系的干燥收缩开裂分析[J ] . 沈阳建筑大学学报:自然科学版,2005 ,21 (5) :519 - 522.
[2] Springenschmid R. Prevention of thermal cracking inconcrete at early ages [ M ] . London : E &FN Spon ,1998.
[3] Czerny F ,Breugel K Van ,Koenders E. The reliabili2ty of crack predictions for hardening concrete struc2tures[C] . / / Global construction ultimate concrete op2
portunities 6th international Congress. London :Thomas Telford ,2005. 757 - 766.
[4] Yuan Y,Wan Z L. Prediction of cracking within early- age concrete due to thermal ,drying and creep be2havior[ J] . Cement and concrete research ,2002 ,32 :1053 - 1059.
[5] 杨伟军,赵传智. 土木工程结构可靠度理论与设计[M] . 北京:人民交通出版社,1999.
[6] ; stlund L. Study of necessary value of the partial co2efficient for load of trains at design of railway bridges[ M ] . Sweden : Swedish Railroad Administration ,1997.
[7] Mats Emborg , Stig Bernander. Assessment of riskthermal cracking in harding concrete [ J ] . Journal ofStructure Engineering ,1994 ,120 (10) :2893 - 2911.
[8] 李铭恩,郭自力,耿川东,等. 混凝土早龄期强度变异性分析[J ] . 河南建材,2001 (3) :38 - 39.
[9] 王甲春,阎培渝. 早龄期混凝土结构的温度应力分析[J ] . 东南大学学报:自然科学版,2005 (S1) :15 -18.
[10] 方东平,祝宏毅,耿川东,等. 施工期钢筋混凝土结构特性的实测研究[J ] . 土木工程学报, 2001 , 34(2) :7 - 10.

















