摘要:静力分析的精确程度对大跨度斜拉桥设计和施工过程具有很大影响。提出一套有限元方法,以弯曲能量作为目标函数确定斜拉索的初始张拉力,通过修正斜拉索的弹性模量,引入几何刚度矩阵和大挠度矩阵,综合考虑斜拉索垂度效应、梁柱效应和大位移效应,采用混合法求解系统方程。程序经过算例验证并应用于在建的重庆大佛寺长江大桥,取得了较好的效果,为该桥的施工控制提供了依据。
关键词:斜拉桥;非线性;垂度效应;梁柱效应;混合法
斜拉桥具有受力合理、造型美观、施工方便等诸多优点,在跨径400~ 1500 m 的范围内,已成为最常见的一种桥梁结构形式。作为一种高次超静定结构,其计算分析的精确程度将直接关系到设计的优劣与施工过程中的安全。
近年来,斜拉桥跨度不断增大,整体结构在恒载及拉索张拉力作用下表现出明显的非线性特征。本 文提出了一套全面考虑斜拉桥几何非线性因素的有限元方法,并在工程实践中得到了验证。
1 斜拉桥的几何非线性特征
斜拉桥几何非线性的产生主要有以下3个来源:1)斜拉索垂度效应;2)梁柱效应;3)大位移效应。
1. 1 斜拉索垂度效应
斜拉索在自身重力作用下产生下垂,其端部位移一部分由材料变形产生,另一部分受拉索垂度影响,造成索力与位移之间的非线性关系。随着张拉力的增加,垂度逐渐减小,轴向刚度不断增大。因此当采用直杆单元建立有限元模型时,必须考虑斜拉索的垂度影响。
采用等效弹性模量能够方便有效的考虑垂度效应,已经得到广泛应用[1,2 ],最早由Ernst 提出的计算等效弹性模量的公式为:
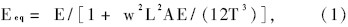
式中:E 为斜拉索材料的有效弹性模量,L 为斜拉索水平投影长度,w 为单位长度上斜拉索重力,A
为斜拉索截面积,T 为斜拉索张拉力。
式(1)得出的是切线模量,当索拉力从T 1 变为T2 时,建议采用式(2)计算斜拉索的割线模量[3 ]:
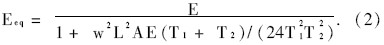
对斜拉索的弹性模量进行修正后,就可以象直杆单元一样建立局部坐标系(见图1)下的索单元刚度矩阵。
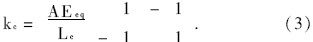
除了上述方法外,还有几种斜拉索的建模方式, 如多段直杆法、曲线索单元法[4 ]等。
1. 2 梁柱效应
斜拉桥主塔及主梁构件均承受巨大轴力。一方面,轴力的存在引起附加弯矩,从而影响杆件的弯曲 刚度;另一方面,弯矩的存在改变杆件的轴向长度,从而影响其轴向刚度。
通过引入稳定函数可以精确地考虑梁柱效应[2],即采用乘数因子对压弯或拉弯杆件的弯曲和轴向刚度进行修正。在局部坐标下(见图2),修正后的梁单元刚度矩阵可表示为:

S1至S6为稳定函数,具体表达式可参考文献[2]。当P=0 时,所有的稳定函数均为1,kb成为忽略梁柱效应的普通单元刚度矩阵。如果把kb中的各项展开成级数形式,例如k33S3项中,当轴向力为拉
力时,有:

因此,当对精度要求不是很高时,利用几何刚度矩阵的修正可以方便有效地考虑梁柱效应。轴向力 为压力时可得到同样的结果。
1. 3 大位移效应
大跨度斜拉桥的计算分析中,结构在较小的应变状态下就会产生较大的位移(可能达到1m以上),对整个结构的内力分布产生很大影响,因而必须采用有限变形理论[5 ],即考虑变形对刚度矩阵的影响,在新的位置建立平衡方程。
在大位移的情况下,应变和位移的关系不再是线性的,即应变矩阵
式中:B0 是线性分析的应变矩阵,而BL 是由非线性变形引起,与位移列阵δ 有关,一般是δ 的线性函数。于是单元的切线刚度矩阵中加入由大位移引起的一项

式中:D 为材料弹性矩阵,对梁单元即为弹性模量E,kL 称为初始位移矩阵或大位移矩阵。
初始位移矩阵的几何意义为:如果在单元变形后的位置建立局部坐标,并将该坐标系下的刚度矩阵变换到未变形的局部坐标中,则经变换产生的矩阵是线性刚度矩阵k0与初始位移矩阵kL之和。
于是综合考虑梁柱效应和大挠度的梁单元刚度切线刚度矩阵为
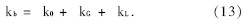
2 理想成桥状态的非线性分析过程
2. 1 斜拉索初始张拉力的确定

为了确定合理索力T i ,首先必须建立优化目标函数。对于预应力混凝土斜拉桥的设计而言,主要是弯矩控制主梁和桥塔的截面尺寸,均匀的弯矩分布可以取得更好的经济效益,因此选取弯曲应变能作 为优化设计的目标函数。将式(14)代入式(15)并忽略式中的剪力和轴力项,得
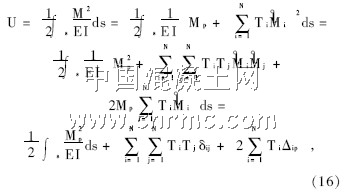

2. 2 非线性问题的求解过程
对于线性结构而言,静力分析的有限元平衡方程为

式中刚度矩阵K 和荷载列阵P 可以按照通用的方法由各个单元的刚度矩阵和节点力组集而成。由于K中的系数为常量,因而节点位移列阵Δ是p的线性函数。对于非线性结构而言,平衡方程仍然具有式 (18)的形式,只是刚度矩阵K 中的系数不再是固定值,变成与结构内力位移有关的函数,而节点位移Δ
是待求的未知量,因此必须采用数值方法求解上述的平衡方程,求出当前荷载作用下结构的平衡位置。
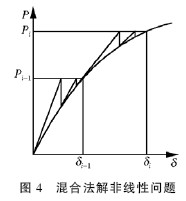
非线性问题的求解一般采用增量法或迭代法。本文将增量法和迭代法结合起来,即采用混合法(图4),荷载分级施加,在每级荷载增量之间应用迭代法,荷载增量可以取大一些,既减少了计算误差,又能够了解受力全过程。按照上述理论,编制斜拉桥非线性静力分析程序。
3 验证算例
利用该程序对文[2]中的非对称斜拉桥进行了计算,模型如图5 所示。其它计算参数如下:弹性模
量E = 191. 352 T Pa;截面惯性矩:主梁I=0. 3884m4 ,上塔柱I=0. 1726m4,下塔柱I=1.726m4;截面面积:主梁A=0.7432m2 ,上塔柱A=0. 2787m2 ,下塔柱A=0.9290m2 ,拉索A=0.1022m2 ;恒载:主梁w=233. 3 kN/ m ,拉索w=4.37kN/ m。
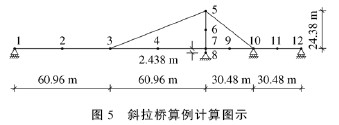
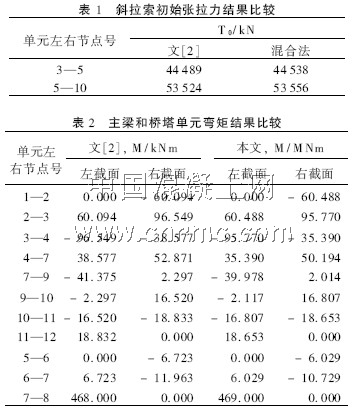
由于采用混合法进行大跨度斜拉桥的非线性分析,因而有效减小了一般增量法造成的累积误差,迭 代次数也比通常的Newton-Raphson 法少,对于非线性较大的斜拉桥同样适用。计算结果见表1、表2。通过比较可以看出,混合法是可靠的。

4 工程实例
重庆大佛寺长江大桥为预应力混凝土双塔双索面斜拉桥,其计算模型如图6 所示。
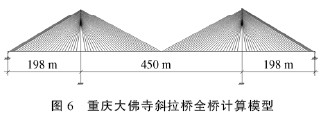
跨度846m,桥面宽30.6m,设计荷载[7]:汽车—超20 级,挂车—120 型,人群3.5 kN/ m2 。主梁为梁板结构形式,梁肋高2. 7 m,采用塔墩固结,塔梁分离的漂浮体系。
为了简化非线性分析过程,特作如下假定:1)所有单元中的应力保持在线弹性范围之内;2)斜拉索
两端分别固定在主梁和桥塔的锚固点上;3)斜拉索视为完全柔性,忽略其抗弯刚度。
主要控制截面内力与变形结果为:跨中挠度7. 46 cm,弯矩9. 82 MNm,塔顶水平位移9. 73 cm, 塔底弯矩127 M Nm。
5 结 论
对于跨度超过400 m 的斜拉桥,斜拉索垂度、梁柱效应及大挠度引起的整体结构几何非线性是明显的,特别在施工阶段,斜拉索张拉力较小时,受力状态比较危险。通过对斜拉索弹性模量的修正,引入初始位移矩阵和初始应力矩阵,可以方便有效地考虑上述非线性因素的影响。以弯曲能量最小为优化目标可以确定出斜拉索在理想成桥状态的初始张拉力。
参考文献:
[1] N azmy A S, Abdel-Ghaffar A M . T hree-dimensional nonlinear static analysis
of cable-stayed bridges [J]. Compu & Struc,1990,34:257 271.
[2] W ang P H, T seng T C, Yang C G. Initial shape of cable-stayed bridges
[J]. Comp u & S truc,1993,47:111123.
[3] 严国敏. 现代斜拉桥[M ]. 成都:西南交通大学出版社, 1996.
[4] Jayaraman H B,Knudson W C. A curved element for the analysis of cable
structures [J]. Comp ut & S truct,1981,14: 325 333.
[5] 赵振铭,陈宝春. 杆系与箱型桥梁结构分析及程序设计[M ]. 广州:华南理工大学出社,1997.
[6] 杜国华,姜林. 斜拉桥的合理索力及其施工张拉力[J]. 桥梁建设,1998,(3):11 17.
[7] 姚玲森. 桥梁工程[M ]. 北京:人民交通出版社,1985.

















