摘要：本文通过一钢筋混凝土框筒结构实例，用振型分解法按等效单自由度体系求解其滞回输入能；用pushover 法分析了滞回耗能在层间的分布规律；根据楼层滞回耗能与弹塑性层间位移的关系求出了各层的弹塑性位移，并通过层间耗能分布及弹塑性层间位移的比较，体现了翼缘框架对整个结构的贡献。以上过程通过与非线性动力时程分析的对比，证明了方法的可行性。
关键词：钢筋混凝土框筒结构；pushover 分析；层间能量分布；弹塑性层间位移
1 前言
自20 世纪50 年代Housner 提出能量法的概念以后，越来越多的研究者开始从地震能量输入与结构能量耗散间的相互关系来分析研究结构的地震反应及其损伤水平。正确揭示地震反应中结构的能量吸收与耗散之间的本质关系，合理地利用其内在联系来控制结构的地震反应及破损，对有效地实现抗震性能设计控制具有很好的应用前景。
多年来，各国研究者在结构的总输入能、滞回耗能的计算及其相应影响因素等方面作了大量的研究[1]~[5]，但对以下几个问题则研究较少：滞回耗能在结构内部的分布规律；弹塑性层间位移作为衡量结构在罕遇地震作用下破坏程度的重要指标，它与层间耗能的关系如何算等。本文采用pushover法分析了滞回耗能在层间的分布规律；根据层间滞回耗能与弹塑性层间位移的关系[6]求出了各层的弹塑性位移。以上结果均与非线性动力时程分析结果进行了对比，证明了方法的可行性。
2 结构输入能计算的振型分解法
框筒结构的平面图及剖面图分别见图1 和图2。层高3m 共12 层，柱距均为3m，角柱截面为700×700mm，其它柱截面为400×600mm，框筒梁截面均为300×800mm,楼板为密肋楼盖。混凝土等级为C30，钢筋选用HPB235 及HRB400 热轧钢筋。采用广厦建筑结构CAD9.0 按7 度设防计算其配筋。
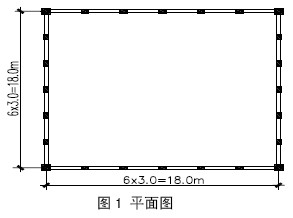
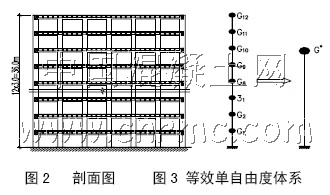
2.1 等效单自由度体系各相关参数的求解
利用等效单自由度体系计算多自由度体系的各能量项时，大都采用一阶等效来求解。本文通过求解该框筒结构各阶等效单自由度体系的滞回耗能(当后一阶能量项的贡献可以忽略时，则不再求解)，认为把二阶等效的结果考虑进去以后，即能给出满意的结果。
以一阶等效为例，各参数求解如下：
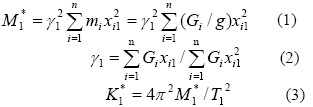
式中：M*1为第1 阶振型的等效质量；K*1为第1 阶振型的等效刚度； γ1 为第1 阶振型的参与系数；Xil为第1 阶振型i 质点的水平相对位移；Gi为集中于质点i 的重力荷载代表值；mi为第i 层的质量；T1为第1 阶振型的自振周期。其它各阶参数可相应求解。
2.2 等效单自由度体系滞回输入能的求解
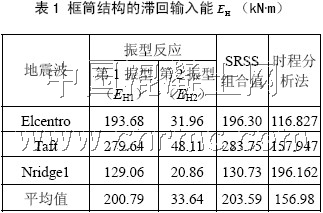
将多自由度体系等效为单自由度体系以后，即可根据其能量方程求解出相应的滞回耗能。本文通过输入以下三条地震波：1940 年南北向EL Centro 波，1952 年69°Taft 波和1994 年90°Northridge 地震波，将各地震波前二阶组合结果的均值作为该框筒结构的等效滞回输入能并与相应的非线性动力时程分析做了对比，从表1 中看出，由于没考虑结构的空间作用效应，时程分析求得的滞回耗能比采用等效单自由度体系的要小。
3 结构层间耗能计算
滞回耗能在结构内部的分布首先是研究其在层间的分布规律。本文采用Pushover方法，给出了一种计算结构滞回耗能沿层间分布的简化计算方法，并与非线性动力时程的计算结果进行了比较。
按照文献[7]的等代角柱法将框筒结构转化为等效的平面框架，采用非线性静动力分析程序IDARC2D5.5 作push-over分析，通过单向单调加大侧向荷载，使结构由弹性状态逐步达到某个预先定义的极限状态为止。本文中定义结构的极限状态为：某构件先于结构达到破坏，或结构弹塑性层间位移超限，或结构成为机构。当达到以上任一极限状态时，则push-over分析结束，认为此时结构已经破坏，取其上一步加载所求得的结构耗能作为结构的极限耗能。结构耗能按以下公式计算：
结构开裂以后，任一构件（梁、柱）在单位步长的耗能为：
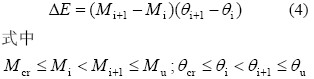
则结构达到预先定义的极限状态时的总耗能为：
对结构作push-over 分析时，研究者们已提出了多种不同的水平加载模式，其中幂级数水平加载模式[8]可以较好地反映结构在地震作用下高振型的影响。其数学表达式为：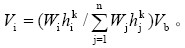
其中，Vi为第i层的层剪力； Wi, Wj分别为结构第i,j层的楼层重力荷载代表值；hi,hj 分别为结构第i,j层楼面距地面的高度；Vb为结构的基底剪力；n为结构总层数；指数K规定如下：当T ≤ 0.5s时，k = 1.0 ；当0.5s < T < 2.5s时，k = 1.0 + (T − 0.5) / 2.0；k = 2.0 T ≥ 2.5s；其中，T为结构基本周期。
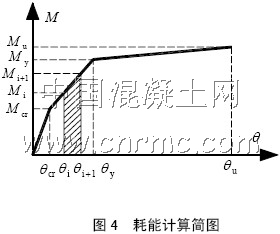
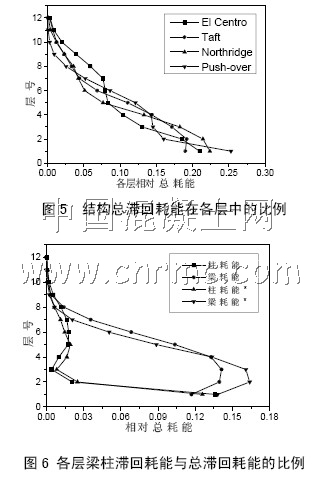
图5 给出了该框筒结构利用push-over法求得的各层滞回耗能与总滞回耗能的比例关系，并与非线性动力时程的结果作了比较。从图5 中可以看出，采用push-over法对结构的总滞回耗能在层间进行分配与非线性动力时程分析结果较为接近，可视为非线性动力时程分析的中间值，因而认为该 法是可行的。
框筒结构中，翼缘框架对整个结构的贡献通过等代角柱而实现。本文还按框筒原角柱截面求解了其各层梁柱滞回耗能与总滞回耗能的比例关系。如图6 所示，带*号的即为按原角柱截面的计算结果，反之则为按等代角柱的结果。从图中可以看出，在该框筒结构中，梁为主要耗能构件；当不考虑翼缘框架作用时柱的耗能变化不大，但会使4层以下梁的相对耗能有较大增加。
4 结构弹塑性层间位移计算
弹塑性层间位移是衡量结构在罕遇地震作用下破坏程度的重要指标，文献[6]中给出了结构楼层弹塑性变形耗能与弹塑性层间位移的关系如下所示：
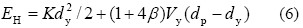
式中：EH 为楼层弹塑性变形耗能；K为楼层侧向刚度；dy 为层间屈服位移； β为滞回耗能系数。对钢筋混凝土结构，取β＝0.33；Vy为按构件实际配筋和材料强度标准值计算的楼层受剪承载力；dp为弹塑性层间位移。
利用结构的层间滞回耗能结合公式(6)即可求出结构的弹塑性层间位移。
图7 给出了该框筒结构采用本文的能量法求得的弹塑性层间位移，并与现行建筑抗震设计规范[8]中的非线性动力时程法和弹塑性位移增大系数法（以下称规范公式）的结果进行了对比。从图中可以看出，除了7 层以上结果相差较大外，在结构相对薄弱也即滞回耗能相对集中的1 至6 层，采用能量法所得结果与抗震规范中的两种方法很接近，与两者的平均值最大相差8.7%。
图8 给出了该框筒结构不考虑翼缘框架作用时的弹塑性层间位移。从图中容易看出，不考虑翼缘框架作用时，框筒结构的弹塑性层间位移比考虑翼缘框架作用的结果要大，最大处相差为9.1%。
5 结论
（1）对于钢筋混凝土框筒结构，可以采用Pushover 法来求解结构滞回耗能在层间的分布。与非线性动力时程需要选取地震波相比，采用Pushover 法可以减少分析时间，同时获得较为稳定的分析结果。
（2）通过等效单自由度法求得的结构滞回耗能及其在层间的分布规律，可以求得结构各层的滞回耗能。结合公式(6)即可求解结构在罕遇水平地震作用下的弹塑性层间位移。
（3）对于钢筋混凝土框筒结构，通过等代角柱考虑翼缘框架的作用可以减少其薄弱层的能量集中，从而使弹塑性层间位移相应减少。
参考文献
[1] Peter Fajfar. Capacity spectrum method based on inelastic demand spectra
. Earthquake Engineering and Structural Dynamics.1999,28:979 -993
[2] Uang C，Bertero V V. Evaluation of seismic energy in structure．
Earthquake Engineering and Structural Dynamics．1990,19: 177-190
[3] Gaetano Manfredi. Evaluation of seismic energy demand. Earthquake
Engineering and Structural Dynamics．2001, 30:485-499
[4] Peter Fajfar,Tomaz Vidic. Consistent inelastic design spectra.:hysteretic and
input energy. Earthquake Engineering and Structural Dynamics．1994,23:523-537
[5] Andre Filiatrault,Pierre Leger,Rene Tinawi. On the Computation of seismic
energy in inelastic structures.Engineering Structures.1994,16(6) ： 425-436
[6] Lieping Ye and Shunsuke Otani. Maximum seismic displacement of
inelastic systems based on energy concept[J]. Earthquake Engineering and Structural Dynamics．1999,28:1483-1499.
[7] 崔鸿超.框筒 (筒中筒 )结构空间工作分析及简化计算.建筑结构学报,1982 ,3(2):32- 41.
[8] Federal Emergency Management Agency.Guidelines and Commentary
for the Seismic Rehabilitation of Buildings. FEMA 273 ＆274,1998
[9] 中华人民共和国国家标准．建筑抗震设计规范GB 50011-2001[M].北京:中国建筑工业出版社，2001.
