摘要:为了进一步探讨复杂加载路径下钢筋混凝土L 形柱的受力性能,采用基于有限单元柔度法纤维模型梁柱单元,对忽略剪切和扭转影响的钢筋混凝土L 形柱在不同加载路径下的抗震性能进行了计算机模拟分析,研究了不同加载路径对钢筋混凝土L 形柱承载力、延性、累积滞回耗能等的影响。结果表明,现有钢筋混凝土L 形柱抗震性能评定方法应作适当调整,以考虑加载路径对评定结果的影响。
关键词:钢筋混凝土柱 加载路径 抗震性能
1.引言
目前国内外对钢筋混凝土框架柱在双向任意加载路径下的受力性能已有一定的研究[1-3],但仅限于对普通矩形柱的研究,对L形柱的研究也只限于沿某一工程轴或斜向加载下的受力性能上[4-7]。这与目前可进行多维拟静力试验的设备、设施较少,特别是试验加载控制较为困难,没有相应的多维加载控制软件有关[1]。由于现有钢筋混凝土L形柱抗震性能的评定主要是建立在沿某一工程轴这一特定的加载路径的试验研究基础之上,为建立和完善钢筋混凝土异形柱抗震性能的评定方法,提供必要的理论依据,有必要对钢筋混凝土L形柱在不同双轴加载路径下的受力性能进行研究。
考虑到目前进行钢筋混凝土L形柱多维拟静力加载试验存在困难,本文采用可同时考虑轴力-双轴弯矩相互耦合作用和刚度退化的纤维模型,编制了相应的非线性分析程序,对钢筋混凝土L形柱在不同加载路径下的受力性能进行了计算机模拟分析,比较了单轴(工程轴)受力和双轴受力时L形柱受力性能的差异,研究了不同加载路径对钢筋混凝土L形柱承载力、延性、累积滞回耗能等的影响。
2.钢筋混凝土L 形柱非线性分析
2.1 计算模型
本文采用基于纤维模型梁柱单元编制的非线性分析程序对不同加载路径下的钢筋混凝土L形柱进行非线性分析,其分析效率和精度已在构件层次和结构层次上分别进行了验证[8-10]。纤维模型将梁柱单元截面离散化为若干纤维,并在假定整个正截面符合平截面假定的同时,假定每根纤维处于单轴应力状态,再根据相应纤维材料的单轴应力-应变关系便可计算截面在多轴加载条件下的复杂恢复力关系。可通过对纤维材料的单轴应力-应变关系的适当修正来考虑箍筋横向约束影响。在此基础上依据有限单元柔度法理论来建立梁柱单元刚度矩阵,避免了传统刚度法理论由于采用单元位移形函数的假定所引起的单元内力分布的准确性问题,对于处理结构或构件进入软化段的材料和几何双重非线性问题,具有很好的效果[10]。有关梁柱单元的形成、单元和截面状态的确定等具体内容,详见文献[10]。
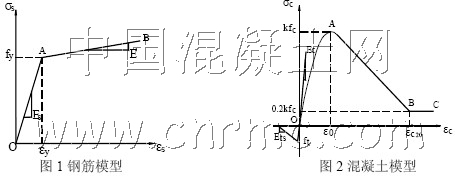
本文中的钢筋模型选用最初由Menegotto和Pinto(1973)所建议后经Filippou等人修改以考虑等向应变硬化影响的双线型本构模型[11],如图1。对于混凝土,采用Scott等人扩展后的Kent-Park模型,如图2 所示。通过修改素混凝土(无约束混凝土)受压骨架线应变软化段斜率来考虑箍筋对混凝土的约束影响。
2.2 计算参数及加载规则
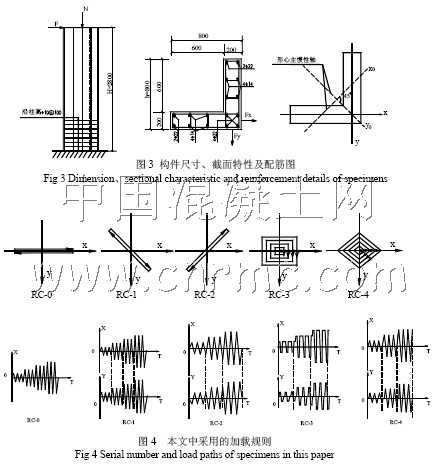
本文对5 根轴压比均为0.2,且有相同尺寸和配筋的钢筋混凝土L形柱在不同加载路径下的抗震性能进行了研究。各构件的混凝土强度等级均为C30,混凝土保护层厚30mm,纵筋强度fy 取值为388N/mm2,箍筋强度fyv 取值为272N/mm2,弹性模量Es取值为2.0×10 MPa,E‘取0.1Es , k 为考虑箍筋约束所引起的混凝土强度增加系数。混凝土模型参数见表1。由于纤维模型目前尚不能考虑扭转、剪切的影响,本文构件剪跨比均设计为H/h=3.5,较实际工程应用有所偏高以保证模拟分析结果的足够准确性[12],同时在进行加载时水平荷载作用点通过截面弯心,即不考虑实际可能同时出现的扭转影响。构件尺寸和配筋如图3。

本文采用位移控制的加载方式,共选用了5 种路径,如图4 所示。以RC-0 作为对比的基准,RC-1~RC-4 分别代表x 与y 轴位移同向、同步、同幅;同步、同幅但不同向;不同步、不同幅但能同时达到各自峰值;不同步、不同幅、不能同时达到各自峰值的四种加载路径,以考察对钢筋混凝土L 形柱抗震性能评定结果的影响。由于钢筋混凝土L 形柱在复杂加载路径下的屈服位移的确定目前仍未有较为一致的规定,为便于与当前钢筋混凝土L 形柱抗震性能评定方式比较,即本文RC-0 加载规则,按此规则以受拉边钢筋首次屈服相应的柱顶位移作为本文的基本位移统一进行加载,并且正反向相同,经计算该基本位移值约为9mm;x、y 分别表示两个垂直的工程轴方向,除RC-1、RC-2 柱x、y 方向均按9mm 施加相同位移外,其余双轴加载构件RC-3、RC-4 都是先加x 向的位移,随后加y 向的位移。x方向加载过程为:第一次幅值为9mm,循环3 圈,然后增加9mm 的幅值,循环3圈,如此 进行;x 方向与y 方向的幅值比为5:4。
3.分析结果
3.1 滞回曲线
各构件的承载力和延性及其他有关数据列于表2,5 种不同加载路径下的钢筋混凝土L形柱的滞回曲线分别示于图5,表中du代表“可用极限位移”,本文定义为最大承载力Fmax下降到85%时相应的位移值。由于在复杂加载路径下构件的屈服位移较难确定,本文中屈服位移dy定义为滞回曲线骨架线上升到最大承载力Fmax的85%时对应的位移,其对应的力为屈服力Fy。μ 为位移延性系数,由du / dy确定。
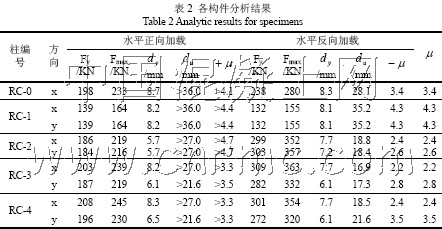
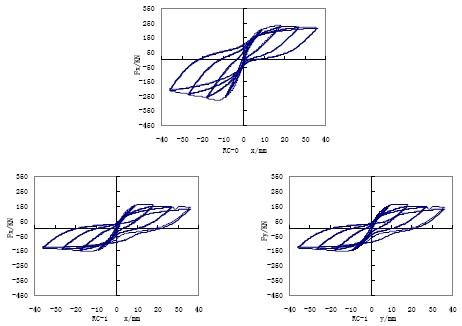
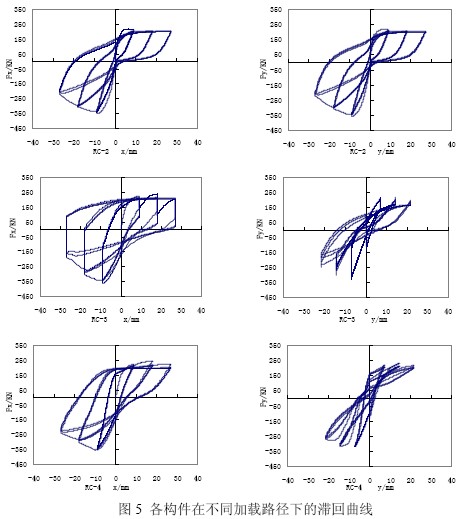
从图5 中可以看出,钢筋混凝土L 形柱滞回性能在双轴加载条件下与单轴加载条件下有明显的不同,如单轴加载后期滞回环呈明显弓形,而双轴加载下却可能为梭形。另外,对于等肢、对称配筋的L 形柱,x 轴与y 轴却可能呈现截然不同的滞回性能,如RC-3。从图5中RC-3 的滞回曲线还可以看出,当x 正向位移加到最大并保持该位移不变时,开始施加y向位移,x 向的承载力有明显下降的现象,而且这种下降随x 向位移幅值的加大而增加,到临近破坏阶段,y 向位移也加到最大值,x 向的承载力几乎下降到零,也就是说到临近破坏阶段,只需要较小的水平力就能保持x 方向的最大位移。这些现象都充分说明钢筋混凝土L形柱与普通矩形柱一样,存在着显著的双轴相互作用,一个方向的加载会引起另一个方向承载力和刚度的降低,且这种影响随着位移幅值的加大更加剧烈。同时由于截面形状的特殊性,较之矩形柱呈现更为复杂、特殊的一些滞回规律。
3.2 承载力及延性
图6 给出了不同加载路径下各构件在x 方向滞回曲线骨架线的对比,从图中可以直观看出不同加载路径对承载力、刚度及延性有明显影响。造成这一现象的原因本质上与普通矩形柱相同:两个正交轴向之间存在强烈的相互耦合作用。从表2 中的数据还可以进一步看出,当采用双轴不同步加载时,x 轴与y 轴最大承载力并不相等,在反向上x 轴高出y 轴约10%,正向上约5%。y 轴加载对x 轴的影响也并非如同普通矩形柱情形总是起到降低承载力的作用,既可能增大也可能降低,有其特殊的一面。

图7 进一步直观地给出了双轴低周反复加载条件下与单调双轴加载条件下x、y 方向承载力Fx-Fy 的对比图。图中虚线为按单调一次加载分析得出的构件承载力包络图,具有明显的对称性,对于非同步加载的RC-3、RC-4(实线)则有一定程度的非对称特点。图7 还表明不论哪种加载路径下,同一根钢筋混凝土L 形柱的承载力总是处于按单调一次加载得出的构件承载力包络图内。尽管加载路径对同一钢筋混凝土L 形柱的极限承载力有一定影响,但考虑双轴相互影响的单调加载承载力是一个较好的近似,也可在此基础上对包络线进行缩减,以便更准确、安全的估计低周反复加载条件下的承载力大小。
对于延性,从图6 和表2 中均可以看出,单轴加载条件下的RC-0 并非总是偏于保守的,除RC1 外,其余三种均明显偏低,并大致接近。这表明延性与加载角有关,RC-2 则有可能是延性较为不利的加载角情形,可起到控制、估计的作用。
3.3 滞回耗能
本文选取表征构件滞回耗能的一个重要指标——等效粘滞阻尼系数来描述构件的滞回耗能。等效粘滞阻尼系数由下式计算:
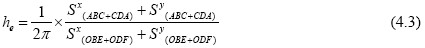
2πhe 表示x、y 方向滞回环实际面积与图8 所示阴影面积之比。
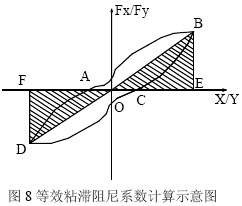
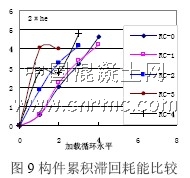
图9 给出了各构件等效粘滞阻尼系数随加载循环水平的变化,图中横坐标的加载循环水平对应于每一种幅值完成一周循环的情形。从图中可以看出,L 形柱在双轴加载路径下其等效粘滞阻尼系数均较单轴加载下的有不同程度的提高, 明显依赖于加载路径,不同加载路径情形之间存在较大差别。造成这一现象的原因,正如文献[1]指出,发生双向弯曲的矩形柱在相同幅值条件下,总的滞回耗能与加载路径的位置和长度有密切的关系,图9表明在L 形柱中也同样有。如RC-3 柱和RC-4 柱的加载规则有相似的加载位置,但是由于RC-3 柱加载路径的长度大于RC-4 柱,因而在滞回耗能上RC-3 柱的等效粘滞阻尼系数均大于RC-4 柱的滞回耗能。
4 结语
本文用基于纤维模型梁柱单元的非线性分析程序,在不考虑扭转、剪切、钢筋粘结滑移影响的前提下,对钢筋混凝土L 形柱在不同加载路径下的受力性能进行了计算机模拟分析。结果表明,钢筋混凝土L 形柱在双轴加载条件下与单轴加载情形有较大的不同,不同的加载路径对L 形柱的承载力、延性、耗能性均有影响。承载力采用单调加载方式估计略为偏高,延性按现有评价方法有可能估计过高,耗能性则与加载路径有较为密切的联系。L 形柱双轴之间存在显著的相互耦合作用,在钢筋混凝土异形柱框架非线性分析中采用考虑此项影响的分析模型是十分必要的。
参考文献
[1] 邱法维,李文峰等. 钢筋混凝土柱的双向拟静力实验研究[J]. 建筑结构学报, 2001, 22(5): 26-31;
[2] 康洪震,江见鲸. 不同加载路径下钢筋混凝土框架柱抗震性能的试验研究[J]. 土木工程学报, 2003, 36(5):71-75;
[3] Bousias S N. Verzeletti G. et al. Load-path effects in column biaxial
bending with axial force[J]. Journal of Engineering Mechanics. ASCE. 1995,
121(5):596-605.
[4] 曹万林, 王光远等. 不同方向周期反复荷载作用下L 形柱的性能[J]. 地震工程与工程振动,
1995,15(1):67-72;
[5] 李杰, 吴建营等. L 形和Z 形宽肢异形柱低周反复荷载试验研究[J]. 建筑结构学报, 2002,23(1):9-15.
[6] 曹万林, 胡国振等. 钢筋混凝土带暗柱L 形柱抗震性能试验研究[J]. 世界地震工程,1999,15(4).
[7] 混凝土异形柱结构技术规程(征求意见稿) [S].中华人民共和国行业标准;
[8] 黄宗明,陈滔. 基于有限元柔度法和刚度法的非线性梁柱单元比较研究[J].工程力学, 2003,20(5):24-31;
[9] 陈滔,黄宗明. 基于有限单元柔度法的钢筋混凝土空间框架非弹性地震反应分析[J]. 建筑结构学报,2004,25(2):79-84;
[10] 陈滔. 基于有限单元柔度法的钢筋混凝土框架结构三维非弹性地震反应分析[ D]. 重庆大学, 2003;
[11] Filippou. F. C., Popo. E. P.v, Bertero.V. V. Effects of Bond
Deterioration on Hysteretic Behavior of Reinforced Concrete Joints[R].
University of California, Berkeley, 1983.
[12] 陈娟,陈滔等. 钢筋混凝土L 形柱分析时平截面假定的适用范围[J]. 地震工程与工程震动 (已录用).
注:
作者:重庆大学土木工程学院 陈滔
重庆市设计院 陈娟 黄宗明

















