混凝土泵车在布料时，由于臂架的伸展与回转，臂架自重对泵车产生的倾覆力矩不断变化。合理确定支腿的展开位置，保证泵车在任一工况下整机的稳定性，对于安全施工具有重要意义。本文从整机重心的轨迹方程入手，以支腿的展开角度为设计参数，确立优化目标函数，确定出评价泵车稳定性的指标。通过对现有泵车参数的实际验算，表明在其它结构未变而仅对展开角度进行调整，泵车的整机稳定性可得到大幅度提高。
1 泵车整机稳定性的探讨
1.1 整机重心轨迹的确定
臂架在展开形式一定的情况下，绕回转中心转动时，整机重心位置的变化规律如图1。
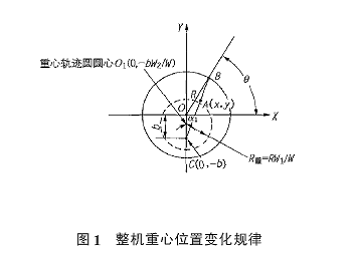
设点A、B、C、O 分别为整机重心、臂架重心、机体重心（除臂架以外的部分）、臂架回转中心在水平面的投影位置。以臂架回转中心O 为坐标原点，O 点与C 点之间的连线为纵轴，建立坐标系。设OB=R，OC=B，臂架在某一位置时与X 轴的夹角为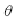 
，则B点的坐标值为B（ Rcos 
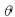， Rsin 
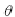）， C点的坐标值为C（O， -b）。根据解析几何和重心理论，其整机重心A 必在B、C 两点之间的连线上，且A（ (xA，yA）点的坐标为：
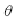，则B点的坐标值为B（ Rcos 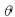， Rsin 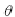）， C点的坐标值为C（O， -b）。根据解析几何和重心理论，其整机重心A 必在B、C 两点之间的连线上，且A（ (xA，yA）点的坐标为：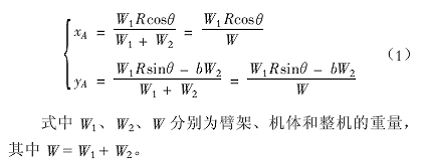
显然，式（1）是以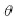 
角为参数的参数方程，消除 
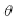角，经变换得：
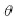角为参数的参数方程，消除 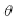角，经变换得：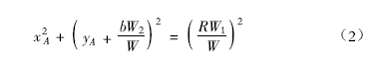
可见，泵车整机重心变化的轨迹为一个圆，圆心O1（见图1）的坐标为（0，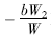 
) ，半径为
。
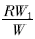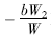) ，半径为 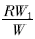。1.2 泵车整机稳定性的衡量指标
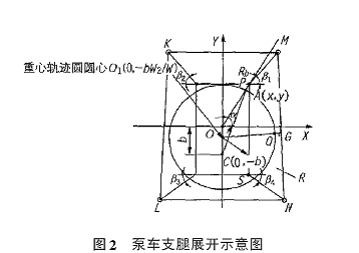
设泵车前、后支腿的转轴位置和支腿长度一定，若前、后支腿的展开角度分别为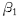 
、
、
、
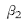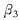（见图2），显然 （ n=1，2，3，4）各角度值的变化范围应为0 ，900，不同的 
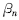值构成了以支腿为4个顶点的不同的四边形支承面。衡量各支腿在某一展开角度时，所构造的支承面对整机稳定性的好坏，先要求出臂架在3600回转时，整机重心距该支承面边缘的最短距离。
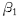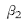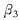、 、 、 （见图2），显然 （ n=1，2，3，4）各角度值的变化范围应为0 ，900，不同的 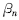值构成了以支腿为4个顶点的不同的四边形支承面。衡量各支腿在某一展开角度时，所构造的支承面对整机稳定性的好坏，先要求出臂架在3600回转时，整机重心距该支承面边缘的最短距离。 先以轨迹圆的圆心点O1为起始点，以点G为垂足，作四边形中的任意一条边如M-N线段的垂线，交轨迹圆于点Q，交线段M-N于点G。设线段QG 的长度值为L1，则L1 为轨迹圆上的点（即臂架回转时整机重心的位置）到线段M-N的最短距离，用同样的方法找出四边形支承面另外3 条边与轨迹圆所对应的最短线段长度L2、L3、L4。比较L1、L2、L3、L4 值的大小，找出4个长度中最短的一个，设该最短距离为S min，即： S min=min｛L1，L2，L3，L4｝，则S min的长度值便可用来衡量此时整机稳定性的指标。显然， S min越大，稳定性越好，反之则稳定性越差。由稳定性理论，各线段长度L1、L2、L3、L4 必须大于零是比较的前提，否则将导致泵车倾翻。
1.3 最佳展开角度所在值域区间的判断
假设支腿的展开角度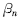 
（ n=1，2，3，4）的数值往两极方向变化，显然，当 
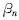值过小（→00）或过大（→900）时， S min值均会减小甚至是负值，由于S min为
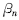的连续函数，因此必有一个 
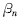［00<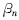 
<900 (n=1，2，3，4)］，可使S min→max，也就是说，支腿按该角度布置展开，泵车的整机稳定性最好。
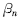（ n=1，2，3，4）的数值往两极方向变化，显然，当 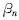值过小（→00）或过大（→900）时， S min值均会减小甚至是负值，由于S min为 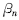的连续函数，因此必有一个 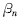［00< 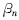<900 (n=1，2，3，4)］，可使S min→max，也就是说，支腿按该角度布置展开，泵车的整机稳定性最好。2 稳定性优化数学模型的建立
2.1 求解整机稳定性的最佳支腿展开角度的步骤
整机稳定性优化数学模型建立的过程也就是按照本文1.1、1.2 和1.3 所说的方法，求得S min、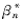 
。需注意2 点：
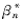。需注意2 点： （1）1.1中所用的方法是在臂架展开形式一定的情况下推导出来的。显然，臂架全部展开且在水平位置回转时，整机重心偏移机体支承面的程度最大，即整机的稳定性最差。因此研究泵车的稳定性问题，就可归结为研究泵车臂架全部展开且在水平位置回转时的稳定性问题，故将臂架全部展开且水平回转时，臂架重心距离回转中心的长度作为（1）式中的回转半径R的数值。
(2）支腿在进行角度调整时，因支腿本身具有重量，因此要考虑支腿重心变动时对机体重心位置的影响。为此，可将泵车分为3 个部分：臂架部分、支腿部分以及车体部分。对于一定的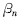 
（n=1，2，3，4），则4个支腿的重心就可完全确定，求出该重心与车体重心的共同重心，并作为式（2）中的机体重心W2，便可利用式（2）求出重心轨迹圆方程。
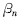（n=1，2，3，4），则4个支腿的重心就可完全确定，求出该重心与车体重心的共同重心，并作为式（2）中的机体重心W2，便可利用式（2）求出重心轨迹圆方程。2.2 稳定性指标的数学表达式
参见图2，设点P、S 与点M、N 分别为相邻两支腿的转轴中心与支承点，RM、RN 分别等于线段PM 和线段SN，则点M的坐标为：
设轨迹圆圆心O1 的坐标为（0，y01），点O1到直线MN 的距离为L1，则：
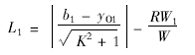
用同样的方法分别求出L2、L3、L4，则该支承状态下，泵车的稳定性指标S min可表示为：
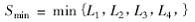
2.3 优化数学模型
综上所述，以4 个支腿展开角度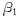
、
、
、
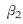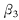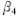为优化设计参数，以稳定性指标（整机重心距离支承面的最小距离）达到最大为目标函数，建立如下表达式：
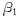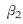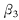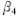、 、 、 为优化设计参数，以稳定性指标（整机重心距离支承面的最小距离）达到最大为目标函数，建立如下表达式：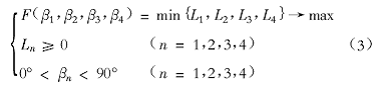
3 计算实例
3.1 优化前后的稳定性对比
就实际使用的泵车而言，大部分泵车的机体结构（除臂架以外的部分）相对于泵车的纵轴线是对称布置的，即机体重心与臂架回转中心均在对称轴上，支腿的展开角度相对于纵轴线也是对称布置的，因此上面所述的4个设计变量可归结为2 个变量，即： = ； = 。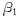
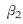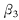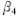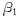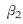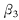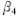= ； = 。 以某单位实际生产的37m泵车为对象，求该泵车稳定性的优化解可使用试凑法（取步长0.10或0.050，其精度足以满足工作需要）或约束变尺度法，输入泵车的其它相关参数（如臂架重心的回转半径和重量值、车体重心的位置和重量值等），得到 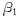、 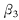的优化设计结果。该泵车原支腿的展开角度和稳定性指标S min与采用优化设计后的支腿展开角度和稳定性指标S min的比较见表1。优化后的S min数值比优化前的增加254mm，增加了53.6%.
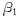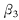、 的优化设计结果。该泵车原支腿的展开角度和稳定性指标S min与采用优化设计后的支腿展开角度和稳定性指标S min的比较见表1。优化后的S min数值比优化前的增加254mm，增加了53.6%.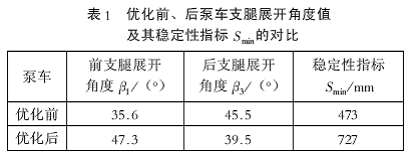
3.2 优化效果
（1）原泵车支腿张开后确定的四边形为矩形，而该最优解为等腰梯形。
（2）避免了常规设计时难以精确考虑支腿本身自重的问题。支腿自重约占整车重量12%左右，因此对稳定性有较大影响。
（3）通过对支腿展开角度的优化，显著提高了泵车整机的稳定性，进而减少因操作等原因造成的泵车倾翻事故。
