摘要:钢筋锈蚀后钢筋与混凝土的粘结强度降低,导致钢筋混凝土柱的力学性能的变化。本文利用APDL参数化设计语言编制的命令流,建立锈蚀钢筋混凝土柱的有限元模型,施加低周反复荷载,获得滞回曲线,分析钢筋锈蚀后柱的滞回性能,与相应试验结论吻合较好。
关键词:钢筋锈蚀,钢筋混凝土柱,ANSYS
1. 引言
柱是钢筋混凝土框架结构的主要受力构件,由于混凝土保护层碳化、钢筋锈蚀、保护层开裂和钢筋与混凝土之间的粘结滑移,柱的承载力性能下降在所难免。主要表现在三个方面[1]:一是钢筋锈蚀引起钢筋截面减小和强度降低;二是钢筋锈蚀将产生体积膨胀,导致混凝土保护层沿筋开裂、甚至剥落,从而使混凝土截面产生损伤;三是钢筋与混凝土之间的粘结性能退化。
强烈地震下结构进入弹塑性状态,地震动输入给结构的大部分能量将在滞回变形中耗散,滞回耗能是结构重要的抗震性能之一。对于锈蚀钢筋混凝土柱的滞回性能,国内外学者也做了相应的试验研究,得到了一些有益的结论[2,3,4,5]。由于钢筋混凝土的损伤裂化速度慢,试验试件无论采用快速碳化锈蚀试验还是自然条件获得,都受到诸多因素的制约。随着计算机技术的大力发展,模拟也在土木工程中大量应用。商业通用程序ANSYS 是一个功能非常强大的有限元分析程序, 具有功能完备的前后处理器、强大的图形处理能力和分析计算能力,在混凝土结构有限元分析中显示出很大的实用性、方便性。本文将在钢筋混凝土损伤劣化研究的基础上,利用APDL参数化设计语言编制的命令流,建立锈蚀钢筋混凝土柱的有限元模型,施加低周反复荷载,获得滞回曲线,分析钢筋锈蚀后柱滞回耗能的变化。
2. 有限元模型的建立
某钢筋混凝土矩形截面框架柱,截面尺寸500×500mm2 。柱高为3600mm。纵向钢筋为HRB335级12φ18 ,沿柱高度方向配置箍筋为HPB235级φ 8@200 ,且在柱底与柱端一米范围内加密为间距100mm。混凝土强度为C30 级,保护层厚度25mm。
为简化模型节约计算资源,又要保证模拟的准确性,特作以下几点假设:混凝土碳化深度为保护层厚度,所以碳化对混凝土强度的影响不予考虑;柱箍筋锈蚀影响不予考虑,假定仍粘结良好,柱纵筋的锈蚀为均匀锈蚀,锈蚀率为7%。
2.1 单元类型的选取
为了更好的模拟钢筋混凝土之间的粘结滑移特性,钢筋混凝土柱采用分离式模型,选择单元有:混凝土-solid65八节点六面体实体单元,钢筋-link8杆单元,钢筋和混凝土之间粘结作用-combin39弹簧单元。
混凝土材料的三维实体单元solid65,由八个节点组成,每个节点具有三个方向的自由度,solid65单元可以模拟混凝土材料开裂、压碎、塑性变形和蠕变的特性。
钢筋选取三维link8单元,该单元有两个节点组成,具有三个方向的自由度。link8单元在工程分析上应用广泛,可以用来模拟桁架、缆索、连杆、钢筋等。这种三维杆单元是杆轴方向的拉压单元,每个节点具有三个自由度,不承受弯矩,具有塑性、蠕变、膨胀、应力刚化、大变形、大应变等功能。
弹簧单元combin39是一个具有非线性功能的单向单元,本单元都有轴向或扭转功能。轴向选项代表轴向拉压单元,每个节点具有三个自由度即沿节点坐标系X、Y、Z 的平动,不考虑弯曲和扭转;扭转选项代表纯扭单元,每个节点具有三个自由度即绕节点坐标轴X、Y、Z 的转动,不考虑弯曲和轴向荷载。
2.2 材料本构关系模型的选取
在钢筋混凝土有限元分析中,准确定义材料本构关系将对计算结果有着至关重要的意义。
在solid65单元中的材料属性需通过定义两个数据表:一个是本构关系的数据表,采用多线性等向强化(MISO)模型描述混凝土应力-应变关系;另一个用于定义混凝土的破坏准则,通过混凝土单元材料特性表定义混凝土的裂缝张开剪力传递系数、闭合剪力传递系数、单轴和多轴抗压强度等9个参数, 定义混凝土的William-Warnke强度准则。本构关系选择混凝土单轴向受压应力应变曲线的E.Honested 建议的模型(公式1~2)。
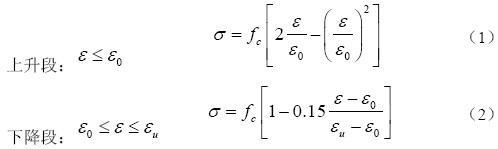
对于模拟钢筋材料的link8单元,定义一个应力-应变关系的数据表,采用双线性等向强化(BISO)模型描述混凝土和钢筋的应力-应变关系。文献[6]通过电化学锈蚀试验并结合非线性有限元分析,给出了锈蚀钢筋名义屈服强度和延伸率的变化规律,本文按其提出的计算公式(3~6)进行分析计算:


用combin39来模拟钢筋和混凝土之间的粘结作用,弹簧性能由弹簧的力—位移(F-D)曲线确定,程序中用实常数20对数表示。
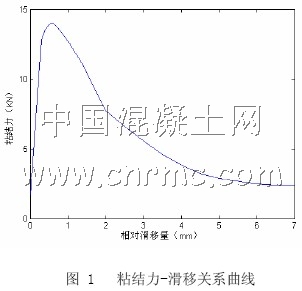
F-D曲线可以通过粘结滑移本构关系τ =τ (s),由以下公式确定,其数学表达式为:F =τ(D)× Ai其中, i A 为该弹簧所对应的在接触面上所占的面积。参考文献[7]通过对试验数据的回归分析,得到完好构件钢筋混凝土的粘结滑移,再利用锈后钢筋和混凝土粘结强度降低系数,得到本文锈蚀钢筋混凝土柱的F-D曲线,如图1所示。
2.3 建模及网格划分
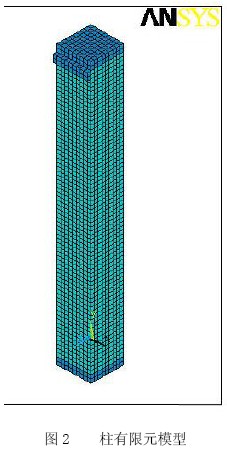
采用实体建模功能直接建模,采用分离模型考虑钢筋和混凝土之间的滑移, 通过三个非线性弹簧单元,分别代表沿接触面平行于纵向钢筋和垂直于纵向钢筋方向模拟钢筋与混凝土间的相互作用,来实现位移协调。网格划分为适当的密度有助于收敛,在建模过程中对单元尺寸进行有效控制,可以有效避免应力集中带来的问题,在钢筋混凝土模型的单元尺寸取5cm。钢筋混凝土柱形状很规则,采用映射方式单元划分,混凝土单元是5832个Solid65 单元,钢筋单元是1908个Link8 单元,钢筋与混凝土的粘结单元是2592个combin39单元。网格划分情况见图2。
2.4 边界约束和加载方式
为防止产生应力集中,在支座和集中力作用处加一个小尺寸的刚性垫块,用Solid45单元来模拟,通过共用节点使刚性垫块节点与相应的混凝土节点位移协调。柱底节点固结,并在柱顶设置定向支座。在柱顶施加竖向荷载,达到轴压比为n=0.3,柱顶端侧面施加单调位移荷载和低周反复荷载两种工况,用位移的∞-范数控制收敛,误差控制可以在2%~3%之间,合理设置子步数,打开线性搜索、预测等项以加速收敛,打开应力松弛开关,加速裂缝即将开裂时计算的收敛。
3. 有限元计算结果分析
3.1 单调加载工况
对有限元模型施加单调荷载:施加水平向 12mm 静位移作用,计算完成后,进入ANSYS的时间历程后处理界面,利用APDL参数化设计语言编制的命令流提取柱底剪力及柱顶位移值,即可得剪力与柱顶位移的关系曲线(如图4所示)。
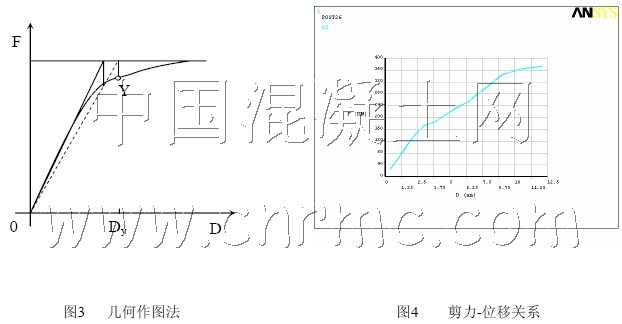
钢筋混凝土柱的屈服点判断是一个比较复杂的问题,国内外尚无统一标准。本文采用文献[8]介绍的几何作图法(如图3所示),Y点为确定的力-变形曲线上的屈服点,对应的Dy为屈服时的构件或结构初始屈服变形。采用此方法可在图 上确定出该柱的初始屈服位移为7.8mm,依据此位移值,可确定钢筋混凝土柱进行弹塑性有限元分析的起始位移可选为7.5mm。
3.2 低周反复荷载工况
对有限元模型施加反复荷载:施加水平向低周反复位移作用,依据单调加载结构的分析,
起始位移选为±7.5mm,逐级加载。计算完成后,进入ANSYS的时间历程后处理界面,利用APDL参数化设计语言编制的命令流提取柱底剪力及柱顶位移值,即可得到该钢筋混凝土柱的滞回曲线(如图5所示)。
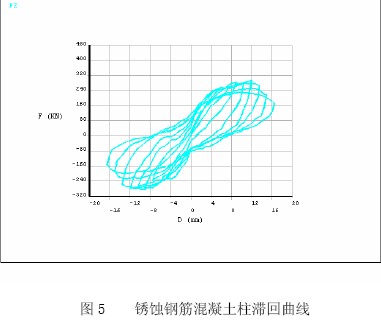
单轴受力构件在循环反复荷载作用下的力-变形曲线称为构件的单轴滞回曲线,简称滞回曲线。在锈蚀钢筋混凝土柱反复荷载作用的剪力位移图,从图上可以看出:
(1)钢筋混凝土柱在开始进入屈服时,加载变形曲线的斜率变化小,卸载后的残余变形也小,正反向加载各一次所构成的滞回环不显,基本上重合为一条直线。
(2)在荷载继续地反复作用,拉应变和压应变不断地积累增大,构件留有残余变形,对粘结弹簧单元影响较大,总的变形持续地增加,而承载变化不大,变形曲线的斜率逐渐减小,这与反复加载下构件的刚度退化有关。
(3)数次反复加载之后,变形曲线上出现了较明显的拐点,形成滞回曲线的捏拢现象,表明滞回耗能能力已经下降。
体系的滞回耗能等于往复循环过程中各滞回环包围的面积之总和,是恢复力在滞回过程
中所耗散的能量。在钢筋锈蚀的情况下,柱的耗能能力降低,抗震性能发生了退化。
4. 结论
利用 ANSYS 有限元软件提供的实体单元SOLID65、杆单元LINK8、弹簧单元Combine39较好的建立了锈蚀混凝土柱的有限元模型,并通过单调加载和低周反复加载,得到了钢筋锈蚀后混凝土柱的力学性能的变化,为进一步建立锈蚀钢筋混凝土柱的恢复力模型提供依据。
本文很好的实现对钢筋混凝土柱的滞回性能仿真分析,与同类型锈蚀构件的试验相比较,也能够取得较为理想的结果。
参考文献
[1]牛荻涛.《混凝土结构耐久性与寿命预测》[M].北京:科学出版社,2003.2。
[2]Okada Kiyoshi,Kobayashi Kazuo, Miyagawa Toyoaki. Influence of longitudinal cracking due to reinforcement corrosion on characteristics of reinforced concrete members. ACI Structural Journal[J].134-140, March-April.1988
[3]颜桂云,孙炳楠,王泽军等.锈蚀钢筋混凝土压弯构件抗震性能的试验研究[J].建筑结构,2003,33(2):16-18。
[4]王学民.锈蚀钢筋混凝土构件抗震性能试验与恢复力模型研究[D].西安:西安建筑科技大学,2003。
[5]刘伯权,刘鸣.钢筋混凝土柱的破坏与能量吸收[J].地震工程与工程振.1998,18(3):14-18。
[6]袁迎曙,余索.锈蚀钢筋混凝土梁的结构性能退化[J].建筑结构学报.1997,18(4):51-57。
[7]徐善华.混凝土结构退化模型与耐久性评估[D].西安:西安建筑科技大学,2002。
[8]张新培.钢筋混凝土抗震结构非线性分析[M]. 北京:科学出版社.2003.9。

















