0 引言
尺寸效应是脆性材料的固有特性。目前国内外关于混凝土材料尺寸效应的研究对象主要集中于索混凝土、钢筋混凝土及预应力}混凝土,并取得了一定的研究成果[1]。对于纤维约束混凝土材料的尺寸效应研究,目前仍处于起步阶段,研究对象大部分是碳纤维布约束的圆柱体试件[2]。方形试件由于存在直角,受力和破坏形式与网柱体不同,强度的尺寸效应也有异于圆柱体试件。关于约束混凝土材料方形试件的尺寸效应研究,澳大利亚的Masia对碳纤维布约束素混凝土方形截面试件的尺寸效应进行了试验研究[3],结果表明试件的轴向峰值应力和轴向峰值应变随试件尺寸的增加而下降。本文通过试验研究了玄武岩纤维布约束素混凝土方柱的尺寸效应,并在试验结果的基础上改进了纤维约束混凝土材料的尺寸效应强度模型。
1 玄武岩纤维布约束混凝土方柱的试验
1.1原材料
水泥选用P·0 32.5级水泥;粗骨料为最大粒径25 mm的卵石,含水率0.244%;细骨料为细度模数为2.22的河砂。外加剂选用江西省创新外加剂有限公司生产的聚羧酸盐高效减水剂LCX-9,掺入量为水泥质量的0.5%;玄武岩纤维单向布由浙江得邦高技术纤维有限公司生产,其规格和性能如表1所示。试验采用的黏结胶水为湖南固特邦土木技术有限公司生产的JN—C碳纤维加同专用胶。

1.2试件设计与制作
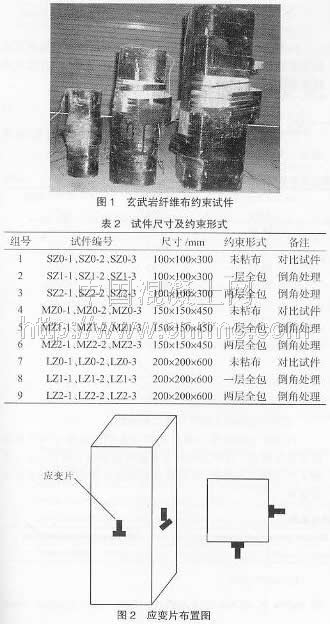
试件为素混凝土方柱,采用标准成型和养护工艺制作而成。试件分为3种不同的尺寸,共分9组,每组有3个试件,总共27个试件。试件如图1所示,立方体抗压强度为50.44 MPa。约束的方柱采用全包的粘贴方式。试件的尺寸及约束形式如表2所示。
1.3加载方式
100 mm×100mm×300 mm的试件采用100 t电液伺服试验机上进行加载,150 mm×150 mm×450 mm及200 mm×200 mm×600 mm的试件在500 t长柱液压试验机上进行加载,加载过程按照GB 50152—1992《混凝土结构试验方法标准》的有关规定进行。正式加载前,先对试件进行物理对中和几何对巾,然后正式分级加载。每级加载为极限承载力的10%,待读数稳定后再读取数据。当加至80%~90%最大荷载后,级差减半,并继续缓慢连续加载,直至试件破坏,
测量试件应变的应变片布置如图2所示..试验中,电阻应变片的应变及百分表数值均通过DH381 9静态测试仪采集。
2试验结果及尺寸效应分析
2.1试验结果
和圆形柱不同,方形柱中FRP约束应力分布是不均匀的,即使试件的角部倒为圆角,其角部的受力仍为最大,所以FRP约束混凝土方柱的破坏通常发生在角部,表现为角部FRP被拉断。
试验得到3种尺寸试件的极限抗压强度如表3所示。一层约束素混凝土方柱的极限抗压强度与未约束素混凝土方柱相比极限抗压强度都有所提高,但提高的幅度都不大,3种尺寸
的极限抗压强度提高幅度分别为22.61%、12.28%、8.34%;二层约束素混凝土方柱的极限抗压强度较未约束的素混凝土方柱相比有了明显的提高,3种尺寸的极限抗压强度提高的幅度分别达39.02%、22.03%、12.46%。

从表3数据中可以发现,粘贴一层BFRP约束素混凝土方柱的极限抗压强度提高的幅度较低,这是由于BFRP约束程度较小,使其应力一应变曲线中出现软化段;粘贴二层BFRP约束素混凝土方柱的极限抗压强度提高的幅度较高,这是由于BFRP约束程度相对来说较大,使其应力一应变曲线中出现强化段,使试件的极限抗压强度得到进一步的提高;在相同的约束层数下,不同试件的极限抗压强度提高的幅度随着尺寸的增大而降低,这说明FRP约束几何相似的素混凝土方柱之间也存在尺寸效应现象,出现这种现象的原因是由于FRP约束大尺寸试件中FRP的用量相对来说较大,出现存在质量问题的FRP纤维的可能性更大,纤维首先在这些地方发生断裂,从而混凝土构件发生破坏。
2.2极限抗压强度的尺寸效应分析
从表3可以看出,玄武岩纤维布约束混凝土方柱的抗压强度存在明显的尺寸效应。相同的约束层数,试件尺寸越大,其强度的测量值越小,不同尺寸约束试件的强度如图3所示。从图3可以看出,3种不同尺寸的未约束试件的抗压强度基本相同,这是因为这3种试件的抗压强度测量值都是同强度等级素混凝土方柱的轴心抗压强度,所以差距不赶;试件约束后,由于纤维布对试件的横向约束,使得不同尺寸试件的抗压强度差距明显,且约束层数越多,抗压强度的尺寸效应越明显。

若以200 mm×200 mm×600 mm试件为标准,其他约束形式与其相同的试件强度与其强度之比为强度换算系数,则得各试件抗压强度的换算系数如表4所示。

2.3纤维约束混凝土试件抗压强度模型及其修正
关于纤维约束混凝土试件的应力一应变关系,国内外已经开展了大量的研究,并提出了一些相关的计算模型。其中具有代表性的有Mander et a1.[4]和Lam and Teng[5]的模型。
Mander et a1.在混凝土多轴破坏面提出的模型基础上,提出了计算纤维约束混凝土的强度模型如下:

式中:fcc一约束混凝土试件的强度,MPa;
fc0一未约束混凝土试件的强度,MPa;
f1-纤维侧向约束强度,MPa。
Lam and Teng在比较已有的强度模型以及对大量的试验数据重新归类整理并进行回归分析,最终得出了一个比较可靠的强度模型,即:
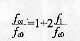
依照式(1)和式(2)对约束混凝土的强度进行了计算,结果如表5所示。

从表5可以看出,Mander模型的计算值明显大于试验值;Lam and Teng模型的计算值和试验值比较接近,但仍存在一些差异。这主要是因为Lam and Teng模型中没有考虑尺寸效应对约束混凝土抗压强度的影响。而在相同的约束程度的情况下,不同几何尺寸的混凝土方柱抗压强度之间明显存在尺寸效应。
针对Lam and Teng模型的不足,本文在试验数据的基础上,对Lam and Teng模型中有效约束系数进行适当的修正,在其中加入与构件几何尺寸有关的参数,从而得到改进的强度模型如式(3)所示。

式中:k1-有效约束系数;
ke-与构件几何尺寸有关的系数。
利用本文的强度计算公式得到各约束混凝土构件的强度如表5所示。其中几何尺寸系数取值如表6所示。由于考虑了尺寸效应的影响,所以修改后的强度模型值更接近于试验结果。

3结论
本文开展了试件尺寸为100mm×l00mm×300mm、150mm×150 mm×450 mm、200 mm×200 mm×600 mm的玄武岩纤维布约束混凝土方柱的抗压强度试验。得到如下结论:
(1)纤维约束试件具有明显的尺寸效应,且随约束层数的增加,尺寸效应更为明显。
(2)以200 mmx200 mmx600 mm试件的抗压强度为基准,其他两种尺寸的素混凝土试件抗压强度换算系数为1.002和0.997;一层约束试件的强度换算系数分别为1.055和1.131;二层约束试件的强度换算系数分别为1.086和1.232。
(3)在原有Lam andTeng模型的基础上,加入了几何尺寸系数。使原有强度模型考虑了尺寸效应对试件强度的影响,从而使该模型更加合理可靠。
参考文献:
[1]黄煜镔,钱觉时.高强及超高强混凝土的脆性与强度尺寸效应[J].工业建筑,2006,35(1):15—17.
[2]YAZIC S,SEZER G I.The effect of cylindrical specimen size on the compressive strength of concrete[J].Building and Environment,2007(42):2417—2420.
[3]MASIA M J,GALE T N,SHIVE N G.Size effect in axially loaded
square—section concrete prisms strengthened using earhon fibre rein—
forced polymer wrapping[J].Canadian Journal of Civil Engineefing,
2004,31(1):1-13.
[4]MANDER J B,PRIESLU M J,PARK R.Theoretical stress—strain model
for confined concrete.Journal of Structural Engineering[J1.ASCE,
1988,114(8):1804—1826
[5]LAM L,TENG J G.Stress—strain models for FRP—confined concrete[D]. Hong Kong:Research centre for advanced technology in structural engineering.The Hong Kong Polytechnic University,2002

















